Intervalo de confianza

Un intervalo de confianza es una técnica de estimación utilizada en inferencia estadística que permite acotar un par o varios pares de valores, dentro de los cuales se encontrará la estimación puntual buscada (con una determinada probabilidad).

Un intervalo de confianza nos va a permitir calcular dos valores alrededor de una media muestral (uno superior y otro inferior). Estos valores van a acotar un rango dentro del cual, con una determinada probabilidad, se va a localizar el parámetro poblacional.

Intervalo de confianza = media +- margen de error

Conocer el verdadero poblacional, por lo general, suele ser algo muy complicado. Pensemos en una población de 4 millones de personas. ¿Podríamos saber el gasto medio en consumo por hogar de esa población? En principio sí. Simplemente tendríamos que hacer una encuesta entre todos los hogares y calcular la media. Sin embargo, seguir ese proceso sería tremendamente laborioso y complicaría bastante el estudio.

Factores de los que depende un intervalo de confianza

El cálculo de un intervalo de confianza depende principalmente de los siguientes factores:

Tamaño de la muestra seleccionada: Dependiendo de la cantidad de datos que se hayan utilizado para calcular el valor muestral, este se acercará más o menos al verdadero parámetro poblacional.
Nivel de confianza: Nos va a informar en qué porcentaje de casos nuestra estimación acierta. Los niveles habituales son el 95% y el 99%.
Margen de error de nuestra estimación: Este se denomina como alfa y nos informa de la probabilidad que existe de que el valor poblacional esté fuera de nuestro intervalo.
Lo estimado en la muestra (media, varianza, diferencia de medias…): De esto va a depender el estadístico pivote para el cálculo del intervalo.

Intervalo de confianza de la media de una población

De una población de media

y desviación típica

\sigma

se pueden tomar muestras de

n

elementos. Cada una de estas muestras tiene a su vez una media. Se puede demostrar que la media de todas las medias muestrales coincide con la media poblacional:

\mu _{\bar {x}}=\mu

Pero además, si el tamaño de las muestras es lo suficientemente grande, o la distribución poblacional es normal, la distribución de medias muestrales es, prácticamente, una distribución normal (o gaussiana) con media μ y una desviación típica dada por la siguiente expresión: $\sigma _{\bar {x}}={\frac {\sigma }{\sqrt {n}}}$ . Esto se representa como sigue: ${\bar {X}}\sim N(\mu ,{\frac {\sigma }{\sqrt {n}}})$ . Si estandarizamos, se sigue que: ${\frac {{\bar {X}}-\mu }{\frac {\sigma }{\sqrt {n}}}}=Z\sim N(0,1)$
En una distribución Z ~ N(0, 1) puede calcularse fácilmente un intervalo dentro del cual caigan un determinado porcentaje de las observaciones, esto es, es sencillo hallar z₁ y z₂ tales que P[z₁ ≤ z ≤ z₂] = 1 - α, donde (1 - α)·100 es el porcentaje deseado (véase el uso de las tablas en una distribución normal).
En esta distribución normal de medias se puede calcular el intervalo de confianza donde se encontrará la media poblacional si solo se conoce una media muestral ( $\bar{x}$ ), con una confianza determinada. Habitualmente se manejan valores de confianza del 95 y del 99 por ciento. A este valor se le llamará $1-\alpha$ (debido a que $\alpha$ es el error que se cometerá, un término opuesto).
Para ello se necesita calcular el punto $X_{\alpha /2}$ —o, mejor dicho, su versión estandarizada $Z_{\alpha /2}$ o valor crítico— junto con su "opuesto en la distribución" $X_{-\alpha /2}$ . Estos puntos delimitan la probabilidad para el intervalo, como se muestra en la siguiente imagen:

\mathbb {P} [{\bar {x}}\geq X_{\alpha /2}]=\mathbb {P} [z\geq z_{\alpha /2}]=\alpha /2

Y en la versión estandarizada se cumple que:

z_{-\alpha /2}=-z_{\alpha /2}

Así:

\mathbb {P} \left[{\bar {x}}-z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {x}}+z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}}\right]=1-\alpha

De lo cual se obtendrá el intervalo de confianza:

({\bar {x}}-z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}},{\bar {x}}+z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}})

Obsérvese que el intervalo de confianza viene dado por la media muestral

({\bar {x}})

± el producto del valor crítico

Z_{\alpha /2}

por el error estándar

({\frac {\sigma }{\sqrt {n}}})

Si no se conoce y n es grande (habitualmente se toma n ≥ 30):⁵

Aproximaciones para el valor

z_{\alpha /2}

para los niveles de confianza estándar son 1,96 para

1-\alpha =95\%

y 2,576 para

1-\alpha =99\%

.⁶

Intervalo de confianza de una proporción

El intervalo de confianza para estimar una proporción p, conocida como una proporción muestral p_n de una muestra de tamaño n, a un nivel de confianza del (1-α)·100% es:

(p_{n}-z_{\alpha /2}{\sqrt {\frac {p_{n}(1-p_{n})}{n}}},\;p_{n}+z_{\alpha /2}{\sqrt {\frac {p_{n}(1-p_{n})}{n}}})

En la demostración de estas fórmulas están involucrados el Teorema Central del Límite y la aproximación de una binomial por una normal.

Ejemplo práctico

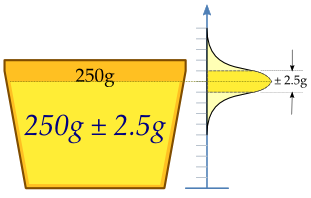
Una máquina llena tazas con helado, y se supone que está ajustada para verter la cantidad de 250 g. Como la máquina no puede llenar cada taza con exactamente 250 g, el contenido que se añade a cada taza individual presenta cierta variación y se le asigna una variable aleatoria X. Se asume que esta variación se ajusta a una distribución normal de alrededor de la cantidad promedio deseada de 250 g, con una desviación estándar de 2.5 g.

Para determinar si la máquina está adecuadamente calibrada, se toma una muestra aleatoria de n = 25 tazas de helado para pesarlas. La medición resultante es X₁, ..., X₂₅, una muestra aleatoria procedente de X.

Para μ, es suficiente con dar una estimación. El estimador adecuado es la media muestral: